Cholesky decomposition

Not long ago I picked up a Matrix Analysis textbook and came across a matrix factorization with this entry's namesake. The Cholesky decomposition factorizes a positive-definite matrix $\mathbf{A}$; $x^{T} \mathbf{A} x > 0$ for all non-zero $x \in \mathbb{R}^{d}$ into a product of a lower triangular matrix $\mathbf{L}$ and its adjoint:

For a positive-definite matrices such a factorization always exists and is unique. The numerical algorithm for constructing the lower triangular matrix $\mathbf{L}$ is relatively straightforward. Initially, the matrix $\mathbf{L}$ begins as a zero matrix with appropriate dimensions. Taking the diagonal elements of $\mathbf{A}$ ($A_{jj}$) and arranging them in a non-increasing order, the algorithm proceeds as follows:

• At step $j$, update the diagonal elements of $\mathbf{L}$ with those of $\mathbf{A}$, $L_{jj} \leftarrow A_{jj}$.
• Update the $L_{ij}$, $L_{ij} \leftarrow A_{ij} / L_{jj}$ for $i = j+1, \ldots, N$.
• Update the stored diagonal elements of $A_{ii}$, $A_{ii} \leftarrow A_{ii} - L_{ij}^2$ for $i = j+1, \ldots, N$
• Increment $j$ and go back to step 1 and repeat until $j$ is equal to index of the last row of the matrix $\mathbf{A}$.

A Python implementation of this algorithm can fit in a tweet

import numpy as np
 
def cholesky(A):
  m, _ = A.shape
  for i in range(m):
      A[i,i] = np.sqrt(A[i,i])
      A[i+1:, i] /= A[i, i]
      A[i, i+1:] = 0
      A[i+1:, i+1:] = np.outer(A[i+1:, i], A[i+1:,i])

The above algorithm can be slightly modified to obtain a low rank approximation of $\mathbf{A}$, by stopping when all the remaining updated diagonal elements $A_{jj}$ are below some specified tolerance $\delta$. For some instances of $\mathbf{A}$, e.g. electron repulsion integrals in quantum chemistry, the rank $\nu$ of the resulting matrix can be much smaller than its maximum possible value.

Here's an animated GIF of what the algorithm does for a $20 \times 20$ positive-definite matrix:

_{Animation of Cholesky decomposition of a 20 by 20 positive-definite matrix. Click to enlarge image.}

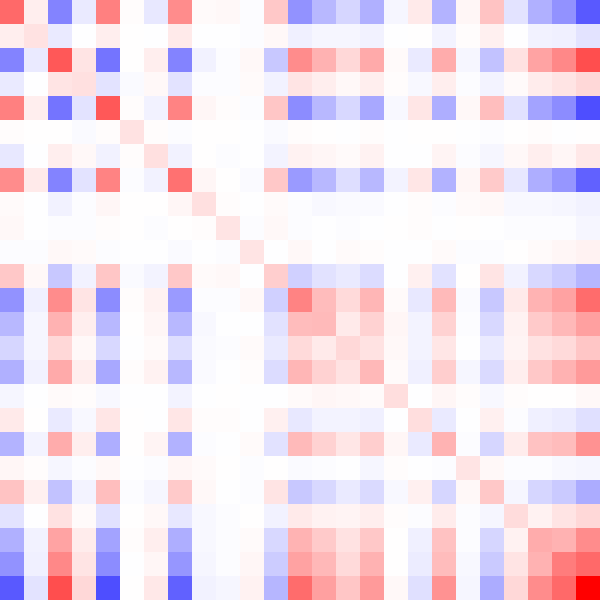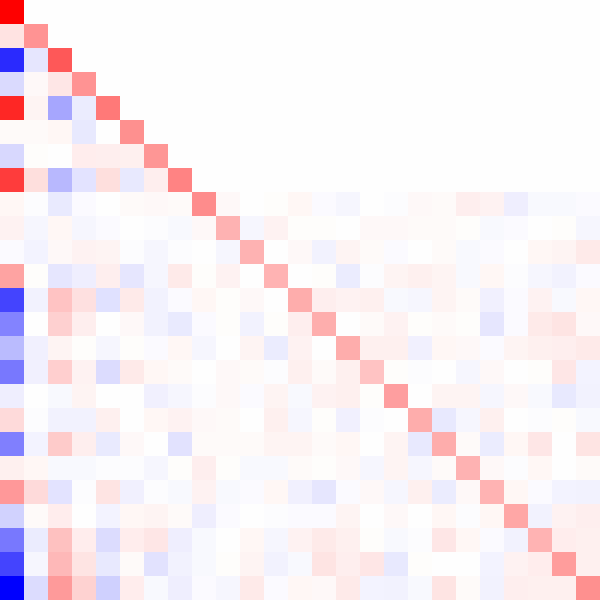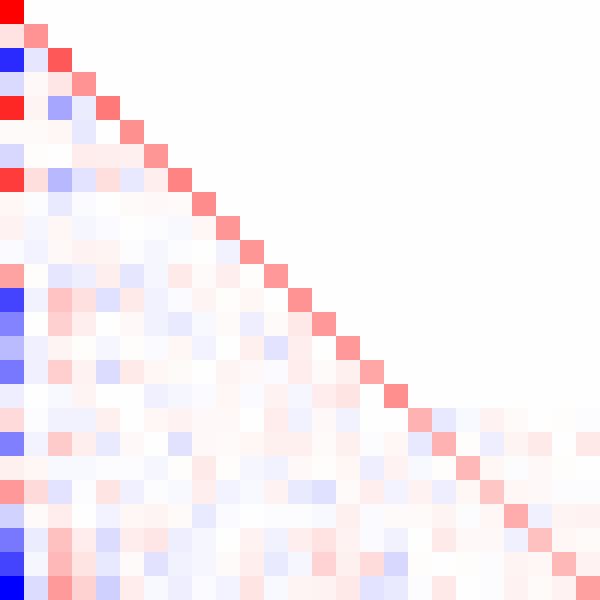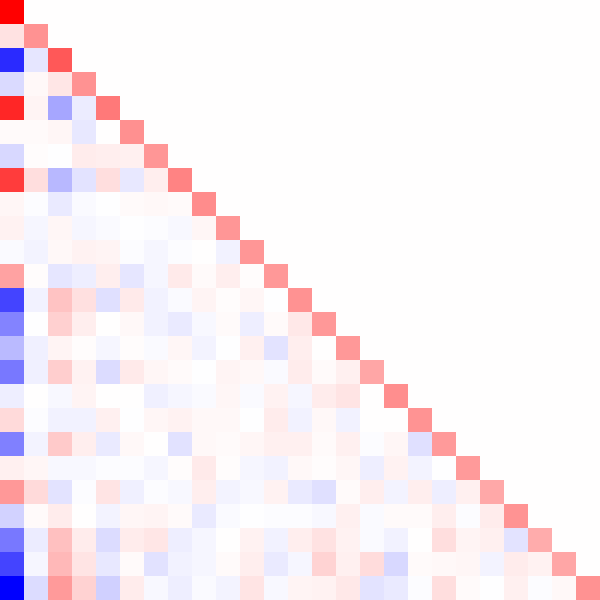
Fin.